Gradient and Spin Echo Pulse Sequences

Gradient and Spin Echo Pulse Sequences#

There are two broad classes of pulse sequences used: gradient-echo and spin-echo methods. Gradient-echo sequences use a simpler pulse and acquire acquisition, while spin-echo sequences use an additional RF refocusing pulse that eliminates the effects of off-resonance that are often undesirable.

Learning Goals#

  1. Describe how various types of MRI contrast are created

    • Describe the difference between gradient and spin echo contrast

  2. Understand the most popular pulse sequences and their acronyms

    • Identify gradient echo and spin echo pulse sequences

  3. Identify artifacts and how to mitigate them

    • Understand the effects of off-resonance and \(T_2^*\) on contrast

Gradient Echo Pulse Sequence (GE or GRE)#

The building block of a gradient-echo (GE) pulse sequence includes an RF excitation pulse followed by imaging gradients. A complete 2D imaging sequence is

Gradient echo pulse sequence

It is called a “gradient-echo (GE)” since the frequency encoding imaging gradients, shown on \(G_X\), are refocused or canceled out at the echo time (more in Spatial Encoding section). Another name for these sequences is a “gradient-recalled echo (GRE)”.

And using a simplified diagram for the gradient echo sequence:

Simplified Gradient echo pulse sequence

The gradient-echo pulse sequence exhibits \(T_2^*\) contrast.

\[S_{GE} \propto M_0 \exp(-TE/T_2^*)\]

Refocusing off-resonance with a spin-echo#

Gradient-echo sequences are sensitive to off-resonance effects and exhibit \(T_2^*\) contrast. However, the effects of off-resonance can be reversed by applying a 180-degree flip angle “refocusing” RF pulse some time after the initial excitation RF pulse. This has the effect of inverting the phase accumulation of off-resonance net magnetizations, after which the off-resonance phase begins to cancel out. This is most easily illustrated in the voxel decay illustrations below:

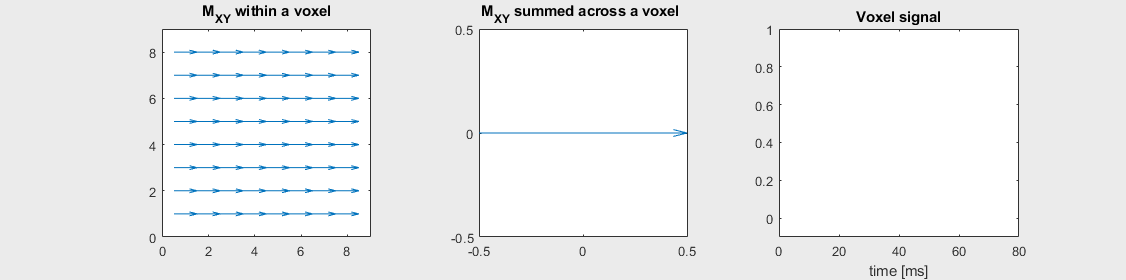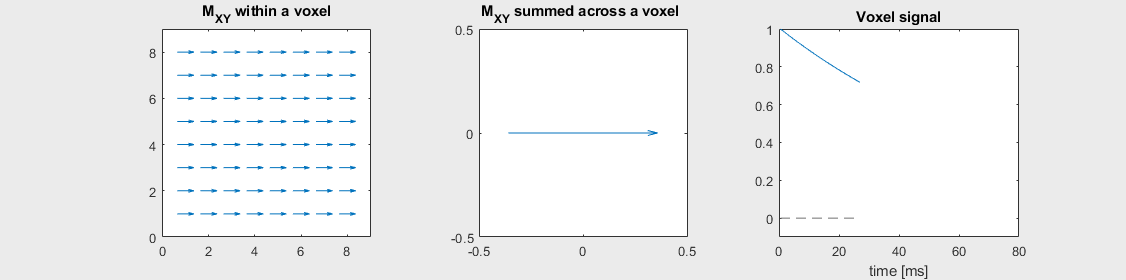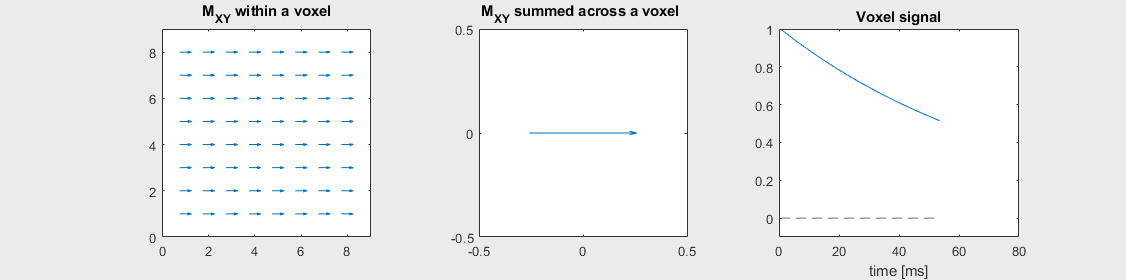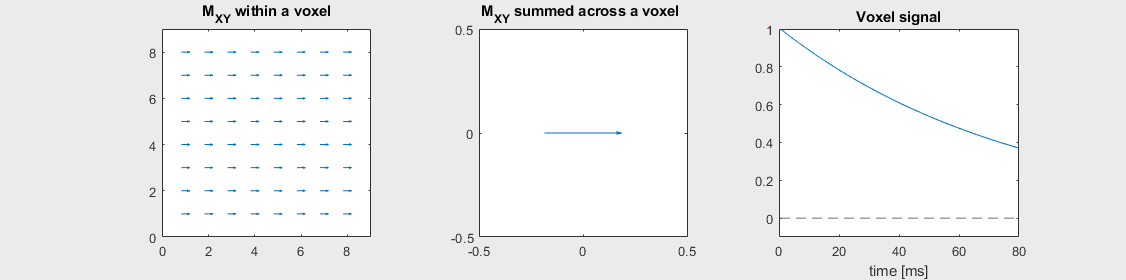
Voxel signal decay, no off-resonance

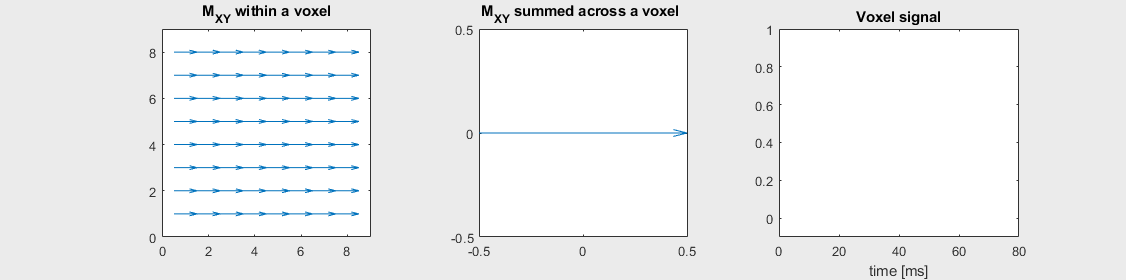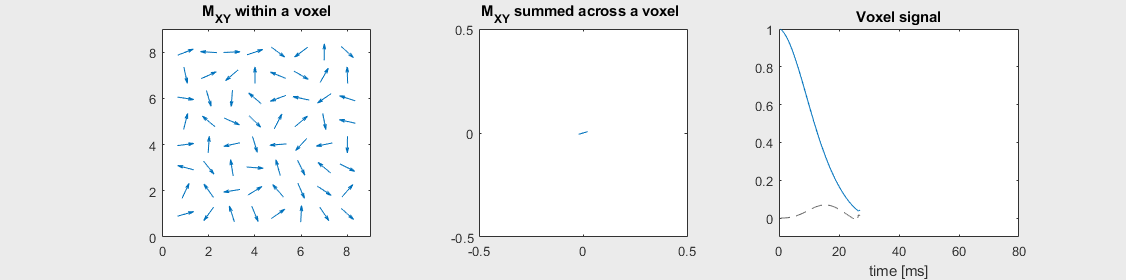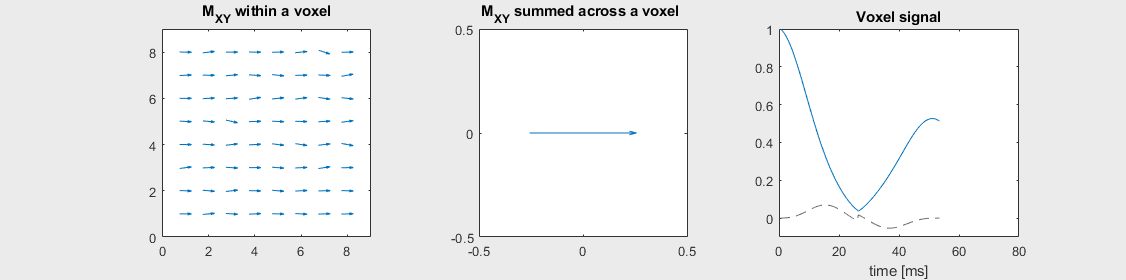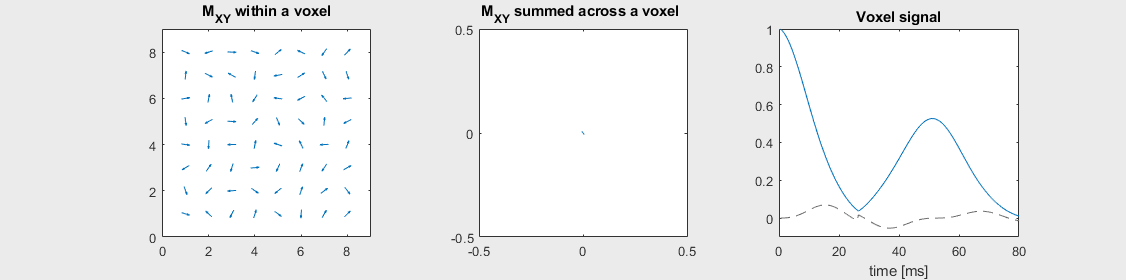
Spin-echo with No off-resonance, \(T_2 = 80\) ms

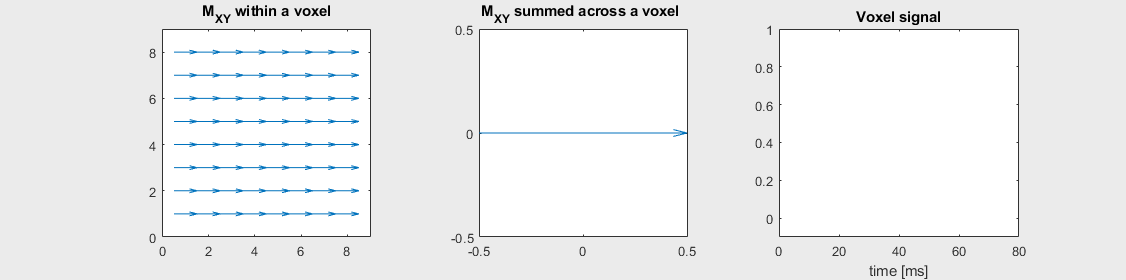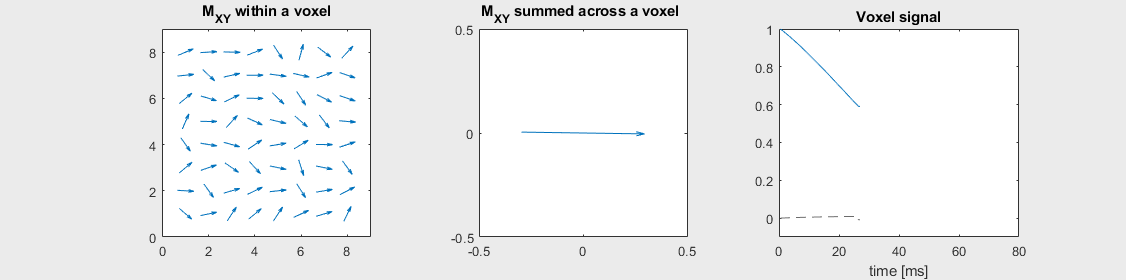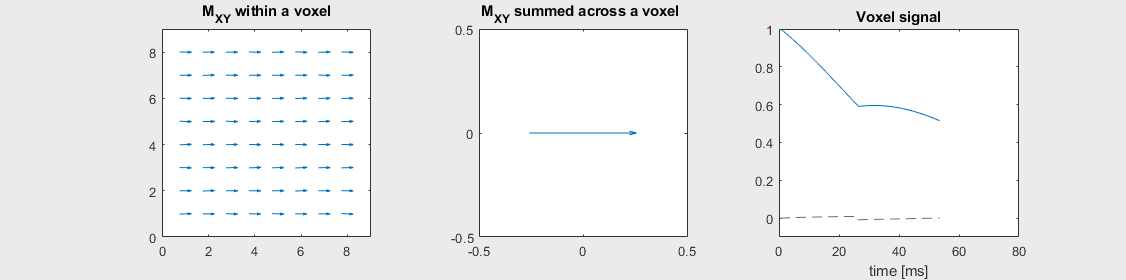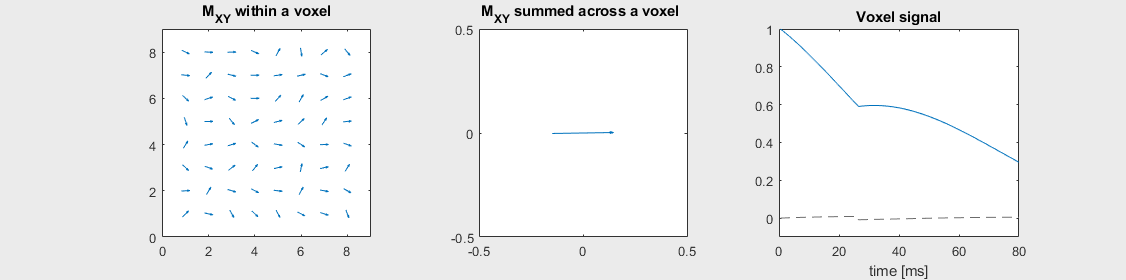
Voxel signal decay, mild off-resonance

Voxel signal decay, severe off-resonance

Spin-echo with Mild off-resonance, \(T_2 = 80\) ms

Spin-echo with Severe off-resonance \(T_2 = 80\) ms

The spin-echo does not make any difference when there is no off-resonance.
Can you identify when the 180-degree refocusing pulse was applied? This is when the \(M_{XY}\) reverts its phase.

Simulation for Visualization of refocusing off-resonance#

To simulate and visualize off-resonance, including various refocusing pulse flip angles, try

  • Visit http://drcmr.dk/BlochSimulator/

  • Scene: Inhomogeneity

  • Apply 90x hard, then 180y hard - what happens to the dephasing spins?

  • Apply 90x hard, then 180x hard - this applies the 180-degree pulse at a different angle. Is there still a spin-echo?

  • Apply 90x hard, then repeated 180s - can multiple spin-echoes be created?

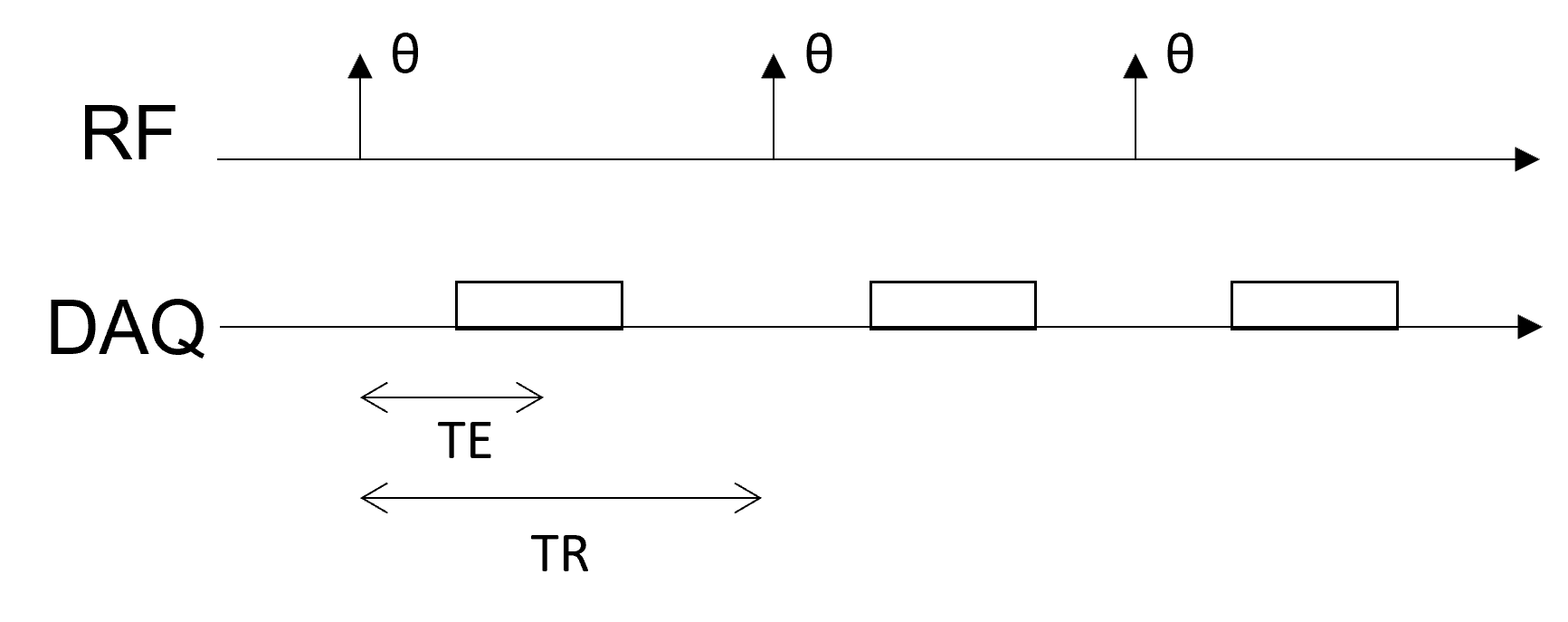
Spin Echo Pulse Sequence (SE)#

The building block of a spin-echo (SE) pulse sequence has an additional 180-degree refocusing pulse between the excitation and data acquisition in order to refocus the effects of off-resonance and create pure \(T_2\)-weighting:

Spin echo pulse sequence

It is called a “gradient-echo (GE)” since the spins are all refocused at the echo time, TE.

This is a simplified diagram for the spin echo sequence:

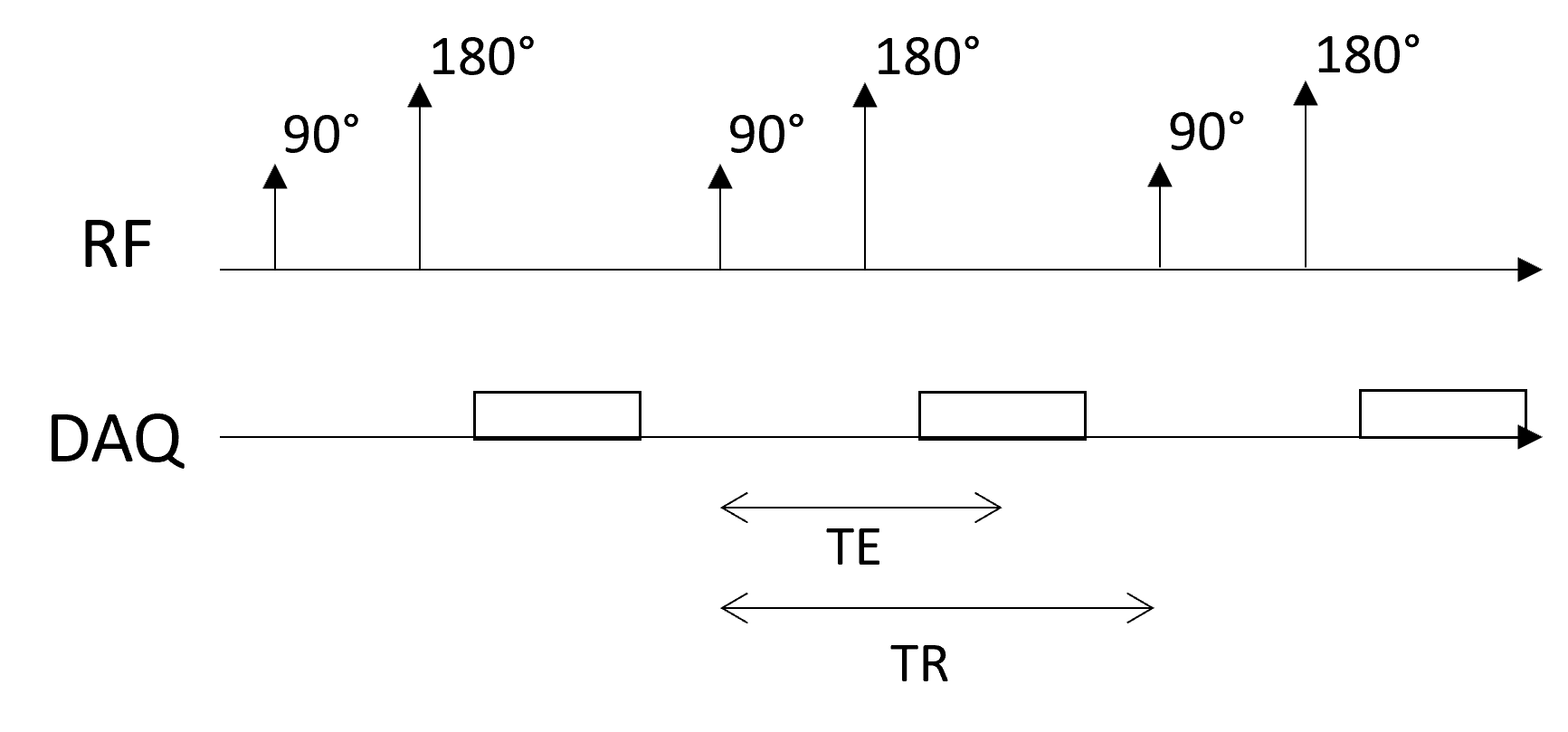
Simplified Spin echo pulse sequence

Because of the refocusing, a spin-echo sequence gives pure \(T_2\) contrast:

\[S_{SE} \propto M_0 \exp(-TE/T_2)\]
Contents