Cartesian Sampling Image Characteristics

Cartesian Sampling Image Characteristics#

The most common type of pulse sequence uses Cartesian sampling on a k-space grid using frequency and phase encoding. Here we explicitly define the image characteristics of FOV, resolution, scan time, and SNR for this sequence.

Learning Goals#

  1. Describe how images are formed

    • Determine the image FOV and resolution when using Cartesian sampling

    • Determine the scan time when using Cartesian sampling

  2. Manipulate MRI sequence parameters to improve performance

    • Determine how Cartesian sequence parameters will change FOV and resolution

    • Determine how changes in sequence parameters will affect the scan time and SNR

Cartesian Pulse Sequence#

The following pulse sequence diagram shows a Cartesian 2D FT sequence including relevant pulse amplitudes and durations needed to determine the image characteristics. A gradient-echo sequence is shown, and the principles can simply be extended to a spin-echo sequence.

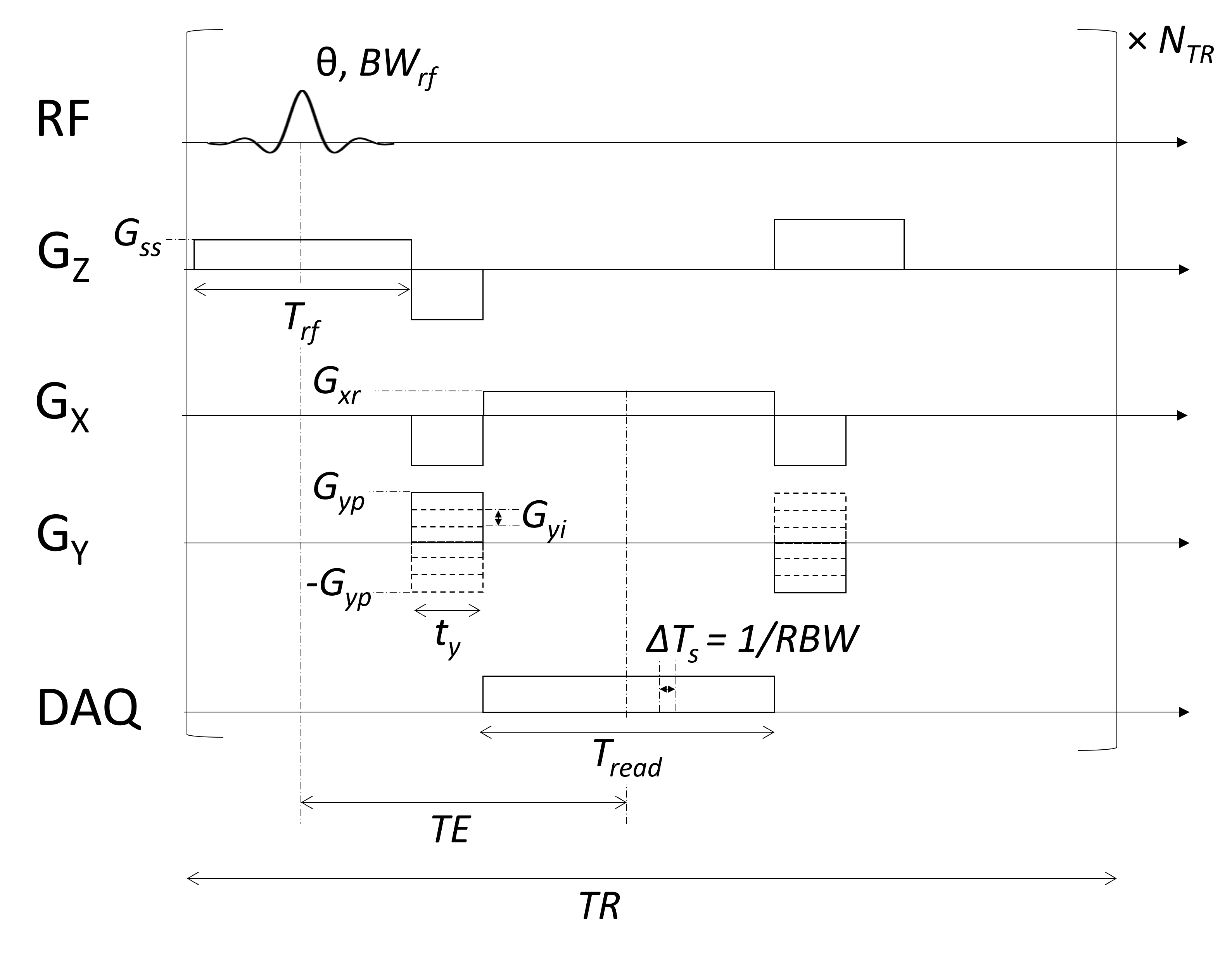
Pulse Sequence Diagram

Note that idealized rectangular gradients are shown for simplicity.

Spatial Resolution#

The spatial resolution is determined by the maximum sample extent in k-space. In the frequency encoding, this can be calculated from the total gradient area during the readout:

\[ \delta_x = \frac{1}{\bar \gamma G_{xr} T_{read}}\]

In the phase encoding, we can calculate the maximum k-space extent bassed on the largest phase encoding gradient area:

\[k_{y,max} = \bar \gamma G_{yp} t_{y}\]
\[ \delta_y = \frac{1}{2 k_{y,max}} = \frac{1}{ \bar \gamma 2 G_{yp} t_{y}}\]

Field-of-View (FOV)#

The FOV is determined by the sample spacing in k-space. In the frequency encoding, this is determined by the sampling rate or the readout bandwidth, \(\Delta T_s = 1/RBW\) and the gradient area during that time:

\[ FOV_x = \frac{1}{\bar \gamma G_{xr} \Delta T_s}\]

In the phase encoding, this is determined by the difference in gradient area between adjacent phase encoding steps:

\[ FOV_y = \frac{1}{\bar \gamma G_{yi} \Delta t_y}\]

All of these relationships can also be rewritten using the relationship between FOV, resolution, and number of voxels.

\[ FOV_x = N_{FE} \ \delta_x\]
\[ FOV_y = N_{PE} \ \delta_y\]

where \(N_{FE}\) is the number of samples in the frequency encoding direction and \(N_{PE}\) is the number of samples in the phase encoding direction.

Scan Time#

For this sequence, the total scan time is determined by the TR and the number of TRs, \(N_{TR}\):

\[T_{scan} = N_{TR} \ TR\]

Assuming no acceleration, the number of TRs is equal to the number of phase encoding steps, \(N_{PE}\), times the number of averages, \(N_{avg}\):

\[T_{scan} = N_{PE} \ N_{avg} \ TR\]

SNR#

The SNR can be written for this sequence in numerous ways using the above relationships. This is left as an exercise to the reader.

Contents